Introduction:

Did you know that approximately 15-25% of data scientists rely on Bayesian Statistics for predictive modeling? Though often seen as complex, Bayesian statistics is a powerful, intuitive approach for refining beliefs based on new data. Meanwhile, sampling distributions are pivotal for statistical inference, enabling confident conclusions from data. These concepts together can feel challenging, but with a clear understanding of their synergy, the path becomes more accessible.

In this blog, you’ll uncover:

• The Basics of Bayesian Statistics: How it updates probability with emerging information.

• The Role of Sampling Distributions: Essential for deriving reliable inferences from data.

Let’s dive into these powerful concepts to fuel your data science journey!

Dive into Bayesian Statistics

The cornerstone of Bayesian Statistics is Bayes’ Theorem, which becomes simpler to grasp through conditional probability. Let’s break down conditional probability before delving into Bayes’ Theorem.

Conditional Probability Simplified

Conditional probability calculates the chance of an event occurring given that another event has already happened. For instance, if you know you’re holding a face card (King, Queen, or Jack) in a deck of cards, what’s the probability it’s a Queen?

• Face Cards Count: 12 (4 Kings, 4 Queens, 4 Jacks)

• Queens Count: 4

With this, the probability is 1 in 3!

Applying Bayesian Statistics

With conditional probability in hand, how does Bayesian statistics actually work in practice? Why is it indispensable in a data scientist’s toolkit?

At its core, Bayesian statistics updates the probability of a hypothesis based on new evidence. Using Bayes’ Theorem, developed by Thomas Bayes, data scientists refine predictions as new data becomes available, in contrast to traditional (frequentist) statistics that rely on static probabilities. Here’s the formula that powers it all:

Where:

• Posterior Probability (P(H|D)): The updated probability that hypothesis HHH is true given data DDD.

• Likelihood (P(D|H)): Probability of observing data DDD if hypothesis HHH is true.

• Prior Probability (P(H)): Initial probability of the hypothesis before data.

• Evidence (P(D)): Total probability of observing DDD across all hypotheses.

Bayesian statistics adjusts the prior knowledge with new evidence, making it adaptable in scenarios where data is ever-evolving or uncertainty is present.

Example

Imagine using Bayesian statistics in medical diagnostics to predict the likelihood of a rare disease. Starting with a 2% prior probability, you adjust it with Bayes’ Theorem as new test results come in, dynamically refining your conclusions. This adaptability proves crucial for evolving insights and precision.

Case Study:

Discover how Bayesian methods enhanced spam filtering techniques. Early spam filters utilized Bayesian models to increase accuracy over time by learning from each piece of new data, resulting in significantly reduced spam detection errors.

Why Bayesian Methods Matter in ML

Bayesian methods have emerged as essential tools in machine learning, offering a dynamic way to improve model predictions and refine decision-making as data evolves. Traditional methods often assume a static set of parameters, but Bayesian inference allows us to constantly update our model’s beliefs with new data. This makes Bayesian approaches particularly valuable for applications requiring adaptability and precision, like predictive modeling, natural language processing, and anomaly detection.

In predictive modeling, Bayesian inference shines by updating predictions as more information becomes available. Imagine a recommendation system in an e-commerce platform: it starts with an initial understanding of user preferences, then continuously refines its predictions with every new click or purchase. Bayesian updating allows the model to adjust to individual users' preferences over time, improving accuracy and relevance in real-time.

For anomaly detection in finance or cybersecurity, Bayesian methods are equally transformative. By setting a probabilistic framework, Bayesian models can assess whether incoming data deviates from typical behavior, even if the nature of normal operations changes over time. This flexibility makes Bayesian methods highly suitable for detecting fraud or cybersecurity threats, where behaviors and patterns are never static.

Moreover, in complex tasks like natural language processing (NLP), Bayesian inference helps models interpret nuances in context as they learn from new texts or phrases, supporting applications like sentiment analysis and language translation.

The beauty of Bayesian methods in machine learning lies in their adaptability. By allowing models to “learn” and refine over time, Bayesian inference supports a level of real-world responsiveness that many traditional methods simply can’t match. As machine learning continues to advance, the importance of Bayesian methods is only set to grow—especially for data scientists aiming to build models that adapt, respond, and deliver with precision in an ever-evolving data landscape.

Sampling Distributions: The Backbone of Bayesian Inference

While Bayesian statistics is about adjusting probabilities as evidence arises, sampling distributions allow confident inferences from gathered data. By mastering sampling distributions, Bayesian applications in real-world datasets become practical and precise.

Understanding Sampling Distributions

A sampling distribution represents the distribution of a statistic (mean, median, variance, etc.) from repeated samples of the same population. Key to this concept is the realization that distributions of these sample statistics help make informed conclusions about the population as a whole.

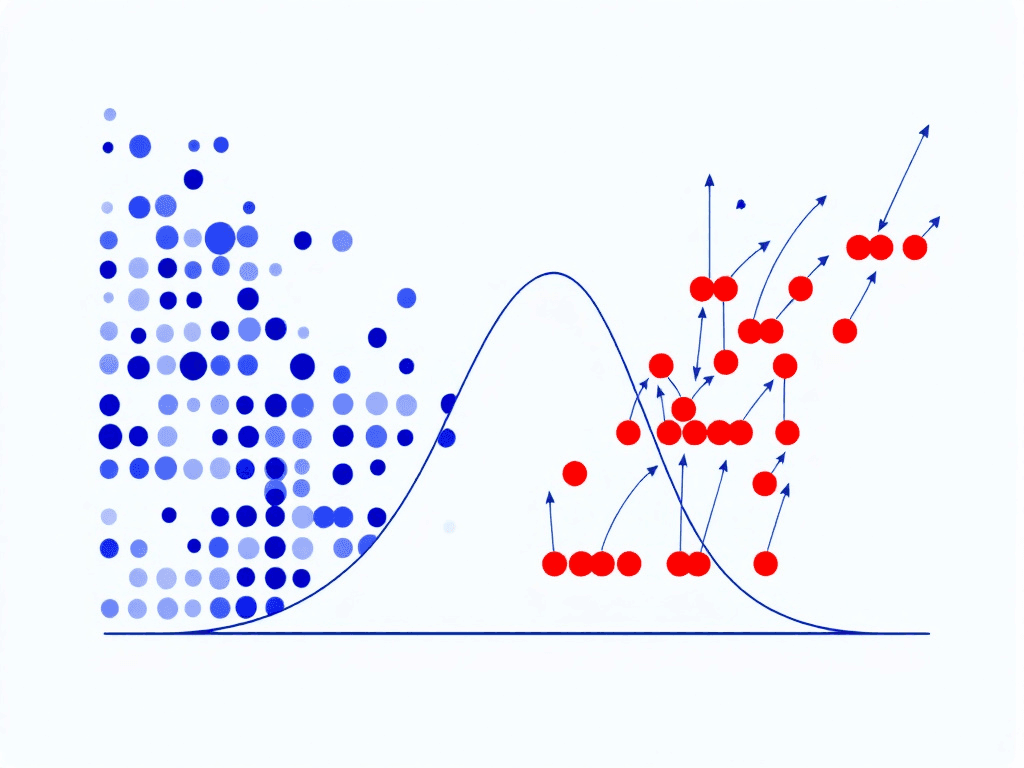
Central Limit Theorem (CLT):

The CLT states that as sample size grows, the sampling distribution of the sample mean approximates a normal distribution, regardless of the original population’s distribution. This powerful property allows inferences about population parameters, even with non-normal populations.

Practical Example

Suppose you want to estimate the average height of adult men in your city. Instead of measuring everyone (impractical), you collect samples of 50 men each. Every sample will differ slightly in mean height, but with enough samples, the distribution of these means will normalize, allowing you to estimate the city’s average height confidently with, say, a 95% confidence interval.

Case Study:

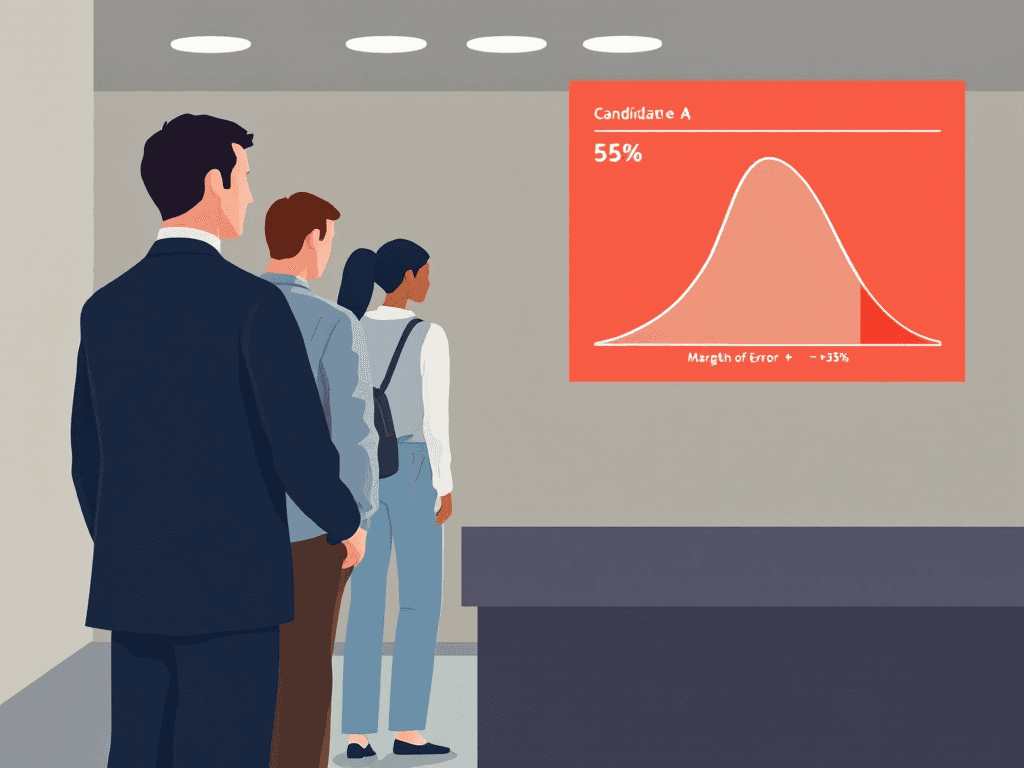
In political polling, sampling distributions are crucial. Pollsters rely on sampling distributions to make confident predictions about public opinion based on sample data, even without surveying the entire population.

Conclusion: Embrace Bayesian and Sampling Methods

Bayesian statistics and sampling distributions aren’t just theory——they are foundational techniques for making data-driven decisions in real-world applications. Mastering Bayesian methods to update probabilities with new evidence, and understanding the role of sampling distributions, prepares you for advanced statistical techniques like ANOVA (Analysis of Variance). While Bayesian statistics help refine predictions based on prior knowledge, ANOVA allows you to identify significant differences between group means, making it an indispensable tool in statistical analysis and hypothesis testing.

Ready to take these insights further? Head over to our Resources Page for free, exclusive workbooks, including your Intro to Statistics eBook and the Bayesian Statistics Workbook. These are packed with hands-on exercises to sharpen your skills instantly—perfect for anyone serious about standing out in data science.

Keep an eye out and Sign Up now below for more exclusive content rolling out soon. Join our community of passionate data minds, dive into actionable insights, and start making impactful, data-driven decisions. Stay tuned, and let’s keep pushing your edge in the ever-evolving world of data science